Legos' writes and shares

Bài toán dừng - Halting Problem

Legos Light's photo
Legos Light
·

4 min read

English version here

Bài toán Dừng, một vấn đề nổi tiếng trong lĩnh vực khoa học máy tính và logic toán học, được hình thành lần đầu tiên bởi nhà toán học và logic học người Anh Alan Turing vào năm 1936. Bài toánđặt ra câu hỏi đơn giản nhưng có ý nghĩa sâu sắc:

💡
Liệu có thể xác định được một chương trình máy tính bất kỳ sẽ dừng lại hay chạy mãi mãi khi thực hiện trên một đầu vào cụ thể không?

Tính Không Quyết Định Và Ý Nghĩa Của Nó

Câu trả lời, được chứng minh bởi Alan Turing vào năm 1936, là không. Không tồn tại một thuật toán chung có thể giải quyết bài toán Dừng cho mọi chương trình và đầu vào có thể. Nói cách khác, không có một "cỗ máy tiên tri" nào có thể dự đoán chính xác hành vi của mọi chương trình.

Kết quả này có ý nghĩa to lớn. Nó không chỉ chứng minh giới hạn của khả năng tính toán, mà còn chỉ ra rằng có những vấn đề mà máy tính không bao giờ có thể giải quyết một cách hoàn hảo. Điều này đặt ra những câu hỏi quan trọng về bản chất của tính toán và những gì chúng ta có thể kỳ vọng từ máy móc.

Chứng Minh Bằng Phản Chứng

Turing đã sử dụng một kỹ thuật gọi là "phép chứng minh bằng phản chứng" để chứng minh tính không quyết định của bài toán Dừng. Ông giả sử rằng có tồn tại một thuật toán có thể giải quyết bài toán này, và sau đó xây dựng một chương trình mới sử dụng thuật toán này để tạo ra một mâu thuẫn logic. Sự tồn tại của mâu thuẫn này chứng minh rằng giả định ban đầu là sai.

Dưới đây là chứng minh cho bài toán dừng (Halting Problem) là không thể quyết định được, sử dụng kỹ thuật phản chứng:

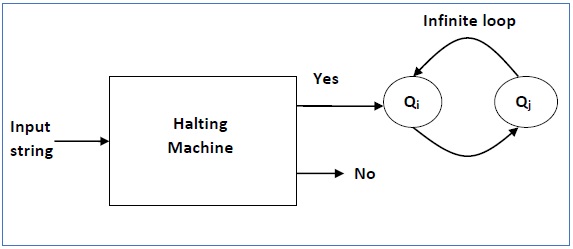
1. Giả định:

  • Giả sử tồn tại một máy Turing (hoặc một chương trình máy tính) H có thể giải quyết bài toán dừng.

  • H nhận đầu vào là chương trình P và một dữ liệu vào w, và đưa ra:

    • "Có" nếu P dừng lại khi chạy với dữ liệu vào w

    • "Không" nếu P chạy mãi mãi khi chạy với dữ liệu vào w

2. Xây dựng máy Turing "phá hoại" D:

  • Ta xây dựng một máy Turing mới gọi là D, hoạt động như sau:

    • Nhận đầu vào là một máy chương trình X bất kỳ.

    • Chạy D với đầu vào là X, trong thân của chương trình D, ta gọi / thực thi chương trình H với đầu vào là X và X

    • Nếu H trả về "Có" (nghĩa là X dừng lại khi chạy với chính nó làm dữ liệu vào), thì D đi vào một vòng lặp vô hạn.

    • Nếu H trả về "Không" (nghĩa là X chạy mãi mãi khi chạy với chính nó làm dữ liệu vào), thì D dừng lại.

H(p, i):
    if (p is halted with input i) return "yes"
    return "no"

D(x):
    if H(x, x) == "yes":
        // tạo vòng lặp vô tận
        while True:
            continue
    else:
        halt // dừng chương trình

3. Tạo ra mâu thuẫn:

Bây giờ, ta xem xét điều gì xảy ra khi ta đưa chính D làm đầu vào cho D (tức là chạy D với dữ liệu vào là D):

  • Nếu H(D, D) trả về "Có":

    • Theo định nghĩa của D, D sẽ đi vào một vòng lặp vô hạn.

    • Nhưng điều này mâu thuẫn với việc H đã xác định rằng D sẽ dừng lại khi chạy với chính nó làm đầu vào.

  • Nếu H(D, D) trả về "Không":

    • Theo định nghĩa của D, D sẽ dừng lại.

    • Nhưng điều này lại mâu thuẫn với việc H đã xác định rằng D sẽ chạy mãi mãi khi chạy với chính nó làm đầu vào.

4. Kết luận:

Trong cả hai trường hợp, ta đều dẫn đến mâu thuẫn. Mâu thuẫn này phát sinh từ giả định ban đầu rằng tồn tại một máy Turing H có thể giải quyết bài toán dừng. Do đó, giả định này là sai.

Ảnh Hưởng Đến Khoa Học Máy Tính

Bài toán Dừng đã có ảnh hưởng sâu rộng đến nhiều lĩnh vực trong khoa học máy tính.

  • Lý thuyết tính toán: Nó là một trong những ví dụ đầu tiên và quan trọng nhất của một bài toán không thể quyết định được, mở đường cho việc nghiên cứu về các giới hạn của khả năng tính toán.

  • Phát triển phần mềm: Nó nhắc nhở các lập trình viên rằng không thể có một công cụ hoàn hảo để phát hiện tất cả các lỗi có thể xảy ra trong một chương trình, chẳng hạn như vòng lặp vô hạn.

  • Trí tuệ nhân tạo: Nó đặt ra những câu hỏi về khả năng của máy móc trong việc tự suy luận và giải quyết các vấn đề phức tạp.

halting-problem