Legos' writes and shares

The Halting Problem

Legos Light's photo
Legos Light
·

3 min read

Xem version tiếng Việt ở đây

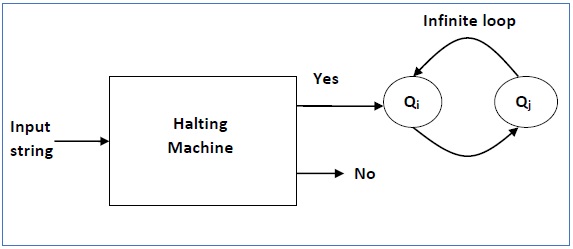
The Halting Problem is a famous problem in the field of computer science and mathematical logic. It was first formulated by the British mathematician and logician Alan Turing in 1936. The problem is not about finding a solution but determining whether a solution exists in the first place.

In simple terms, the Halting Problem can be defined as follows:

Given a description of a computer program and its input, can you determine whether the program will eventually stop (halt) or run forever?

More formally, let's say you have a computer program, and you want to know if running this program on a specific input will result in the program eventually terminating (halting) or if it will keep running indefinitely.

The significance of the Halting Problem lies in its undecidability. Alan Turing's work showed that there is no general algorithm or computer program that can solve the Halting Problem for all possible programs and inputs. In other words, there's no magical "Halting Oracle" that can take any program and input and predict whether it will halt or run forever.

Turing proved this through a clever and self-referential argument. He assumed that there is a program that can solve the Halting Problem for all cases and then showed that this assumption leads to a logical contradiction. This contradiction implies that such a universal halting solver cannot exist.

The Halting Problem has profound implications for computer science and the theory of computation:

Undecidability: It establishes that there are problems in computer science for which we can never build a general algorithm to determine the answer. The Halting Problem is one of these undecidable problems.

Limitations of Computing: The Halting Problem illustrates the fundamental limitations of what computers can and cannot do. There are questions that are inherently unanswerable by algorithms, and this problem exemplifies that.

Use in Theoretical Research: The Halting Problem is a central concept in theoretical computer science and is used to demonstrate the undecidability of various other problems. It serves as a foundational concept in the study of computability and complexity theory.

Practical Implications: While the Halting Problem is unsolvable in the general case, it doesn't mean we can't determine if a specific program halts for specific inputs. In practice, programmers use various techniques and heuristics to analyze program behavior and identify potential issues related to halting.

Proof:

Assumption: Assume, for the sake of contradiction, that there exists a function (or algorithm) H that can decide the Halting Problem for all possible inputs (programs and their corresponding inputs). That is, H(p, x) will return "halts" if the program p halts on input x, and "does not halt" if it runs forever.

G(y):
    if H(y, y) == "halts":
        while True:
            continue
    else:
        halt

The program G takes an input y and does the following:

  • It calls H(y, y) to check if y halts on input y. If H says that y halts, then G(y) enters an infinite loop → contradiction.

  • If H(y, y) says that y does not halts, then G(y) actually halts → contradiction.

halting-problem